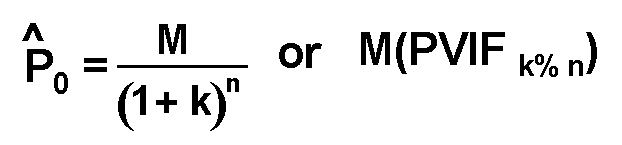
where:
M = par value / face value/ maturity value of bond
k = investor's required rate of return
n = remaining time to maturity of the bond
Bond Valuation
Readings: Chapter 7
At the end of this unit students should be able to:
Identify the key characteristics common to all bonds.
Calculate the value of a bond with annual or semiannual interest payments.
Plot and interpret the Time Path to Maturity of a bond
Explain why the market value of an outstanding fixed-rate bond will fall when interest rates rise on new bonds of equal risk, or vice versa.
Calculate the yield to maturity, and/or the yield to call on a bond.
Differentiate between interest rate risk, reinvestment rate risk, and default risk.
Bonds
are normally long-term debt instruments issued by a company to raise funds. The
bond contract (indenture) states a rate of interest called the coupon rate, a
par value ( face value) and the maturity date
Par
Value this
is the nominal value of the bond when it is issued and most bonds are issued at
a $1,000 par value. This is the sum that the issuer takes from the original
investor and makes a promise to pay at the maturity date while paying interest
during the intervening period. (a discount bond is sold below par and a premium
bond is sold above par)
Maturity
date - this is that future point in time when the
issuer repays the par value of the bond
The
coupon rate is
the bond's rate of interest that is paid to the bondholder. On specific dates a
fixed amount is paid to the bondholder. A coupon interest rate does not change
once the bond is issued
Callable
Bond
2.
Loss of income
There
are usually two classes of Bonds
-
This does not pay any interest during the life
of the bond but is sold at a discount and redeems at par, given by:
|
|
2.
Coupon Bond- given by:
|
|
|
If interest is paid more than once per year
|
|
Example 1
How much will you be willing to pay for a bond with a $1,000 par paying
15% per annum interest if your required rate of return is 20% and the bond
matures in 10 years?
|
|
This is the maximum that you will be willing to pay now for this bond given
your 20% required rate of return. This is so because this is the amount of money
that you could deposit now in an account that pays 20% per annum for the next 10
years to enable you to make 10 yearly withdrawals of $150 plus a $1,000
withdrawals at the end of the 10th year.
The bond sells at a discount because current interest rates are higher
than that reflected in the coupon interest rate attached to the bond. It means
therefore that an investor with money to invest currently can earn more than 15%
per annum and in turn must be compensated for this.
A discount bond is one where the investors required rate of return k is greater
then the coupon interest rate, i.e..
|
k > CIR |
What would you pay for the bond if your required rate of return were 10%
per annum?
|
|
The bond sells above par. In this case the investor's k is only 10% while
he is now getting 15%, so he must pay an extra cost for this.
A premium bond is one where
the investor's required rate of return is less
than the coupon interest rate
|
k < CIR |
Example 3
What would you pay for the bond if your required rate of return were 15%
p.a.
|
|
The price is equal to the par value. Hence when the CIR =
Investor's required rate of return(k), the price of the bond is always
= to the par value. These are called Par Bonds. When bonds are originally
issued they are so done at Par to attract investors.
Let's now look at the price of the bond after one year:
1.
The discount bond:
|
Note- the price has
risen |
2.
The premium bond
|
Note- the price has fallen |
3.
The par bond
|
Note- the price remains the
same |
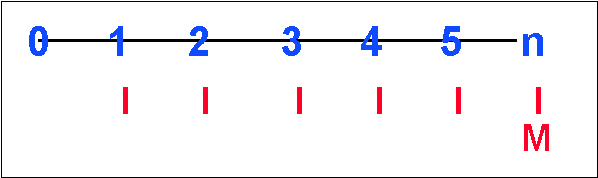
From the above we can see that as the maturity date approaches, the bond
value converges on par ($1,000). This is also expressed by the following graph:
Time Path to Maturity at different discount rates
|
|
This
shows the relationship between price and the remaining time to maturity at a
given discount rate
Interest Rate Risk/Reinvestment Rate Risk/Default Risk
Interest Rate Risk
Recall from our earlier lectures that the likelihood that interest rate will rise is referred to as interest rate risk. Let us now examine what the impact on a bond's price will be given an increase in interest rates.
Using the premium bond our example, we see that the bond was originally priced and issued at $1,307.19 (when the interest rate, k, was 10%). Now let's assume that immediately after the issue (e.g. the very next day), interest rates rose to 12% (i.e. k is now 12%). The price of the bond will now be:
|
|
Therefore if you were to sell these bonds you would effectively lose $137.66 (i.e. $1,307.19 - $1,169.53).
Note - Longer term bonds are exposed to greater interest rate risks as the magnitude of the fall in the price will be much greater than for short term bonds of similar class.
Reinvestment Rate Risk
On the other hand a decrease in interest rates would lead to an increase in your bond's value. However, such a decline in interest rates will bring about reinvestment rate risk. This is the risk that the cash flows received from existing bonds, when reinvested at the lower rates, will result in reduced income for the bondholders. Shorter term bonds are more exposed to reinvestment rate risks than longer term bonds. This is so because not only the interest earned will be reinvested at these lower rates but the principal will also be reinvested at these lower rates when the bonds mature. Only the interest on long term bonds will be exposed to reinvestment rate risks as the principal will normally not mature in the near future.
Default Risk
Recall from our earlier lectures that a default risk premium (DRP) as added to k* for corporations. However none was added for Government instruments. The reason was that corporations are more likely to default on payment than the Government. As far as corporations are concerned, the more likely it is that a company will default on payment, then the higher the DRP will be and in turn the higher the interest rate, k will be.
Yield/Rate of Return
The total yield or total rate of return on a bond a any point in time is equal to the sum of its current yield and its capital gains yield. The current yield is equal to the annual interest payment divided by the previous price and the capital gains yield is equal to the current price - the previous price, all divided by the previous price i.e.
|
|
Therefore using our previous example of the discount bond, the total yield (k) over the first year of its life would be computed as follows :
|
|
Yield to maturity(YTM) / Internal rate of return (IRR)
This
is similar to the preceding discussion and captures the total yield of the investment.
That is, It is the true rate of return if the
investment is held to maturity and each interest payment is reinvested at the
YTM . Assuming that previous statement always holds, a bond's yield to maturity is that interest rate when used to discount the
bond's future cash flows equates them to the current price.
Illustration
Let's
use one of our previous examples again, the premium bond:
CIR=15%,
k=10%, n=10 years, M=$1,000 and Price = $1,307.19
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| $ | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 | 150 |
| $ | 1000 | |||||||||
|
The interest is = 15% x 1000 = $150 which is received annually for 10 years (at year-end i.e. ordinary). Therefore the FV of this interest at T10 is = 150(FVIFA10%,10) = 150(15.9374) = 2,390.61. The holder also receives the $1,000 at T10, thus its FV = $1,000. Now, the total FV at T10 = 2,390.61 + 1,000 = $3,390.61. Analyzing this result we see that the holder paid $1,307.19 for the bond, held it for 10 years and has accumulated $3,390.61. Therefore his effective yield is found by solving for k in the equation: FV=PV(FVIFk%,n). Hence,
|
||||||||||
There
are two ways of estimating the yield to maturity
1.
The Rodriques formu
 |
Note - the version below could also be used (assuming that interest is paid once per year). In fact, I have used it quite a lot in recent times. Also see http://www.e-analytics.com/fp22.htm for its application.
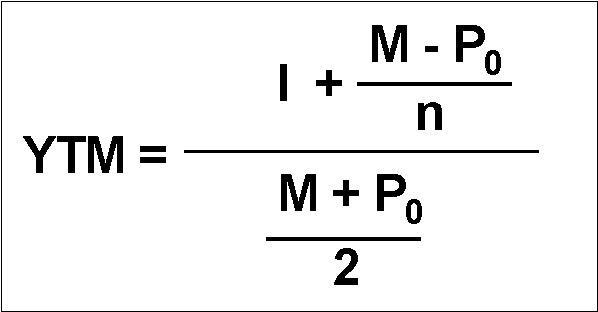 |
|
The distance between A & B divided by the distance between A & C is constant for any values of A, B & C.
|
Class Question
Find the yield to maturity on a bond with 4 years to maturity 8% coupon,
$1,000 par and currently sells at $890.00.
|
We need one price above and one price below:
|
| Interpolating, we get:
|
Note - the Rodriques formula would have given:
|
|
Yield to Call
You will recall that earlier in our discussion we mentioned Callable Bonds. Now bonds are likely to be called if interest rates fall, thereby allowing the issuer to to issue new bonds paying a lower interest. The issuer will use the proceeds of these new bonds to pay-off (retire) the older callable bonds. Now if an investor bought a callable bond and it is likely that interest rates will fall, and therefore likely that the bonds will be called, he is more likely to earn a Yield to Call (YTC) rather than a Yield to Maturity (YTM). This YTC is determined in a manner similar to the YTM, except that the maturity value will not be $1000 but will be the call price. In addition, you will not automatically have as a starting point, a price of $1000 if you were to use k = CIR. (Note - the Rodriques formula could still be used).
Importance of Bond Ratings
Bond Ratings are important both to firms and to investors. First, because a bond's rating is an indicator of its default risk, the rating has a direct, measurable influence on the bond's interest rate and the firm's cost of debt. Second, most bonds are purchased by institutional investors rather than individuals, and many institutions are restricted to investment-grade securities. Thus if a firm's bonds fall below the BBB, it will have a difficult time selling new bonds because many potential purchasers will not be allowed to buy them.[1]
[1] The section has been taken directly from the text, page 290. However, please read pages 286 - 294 for a better understanding.